Mathematics Ph.D. candidate in Victoria BC.

Research

I am broadly interested in combinatorics. My current projects and interests largely fall within combinatorics and graph theory.

combinatorics: classification problems, especially on configurations involving specified or forbidden structure on relations between components; algebraic and matrix methods; connections to musical structures.

graph theory: graph decomposition/covering/packing; graph classification; graph distance.

Graph decompositions

Coming soon (possibly Aug 2026). My dissertation research broadly pertains to graph decompositions.

Graph distances

Coming soon (possibly Jan 2026). I am currently finishing a single-author paper that solves a graph distance multiplicity classification problem.

Boxicity

The boxicity of a graph G is the smallest dimension d such that G can be represented as the intersection graph of axis-parallel boxes in d dimensions. Calculating boxicity is an NP-hard problem for general graphs. Here is an example of a graph G with boxicity 2 and an associated family of boxes.

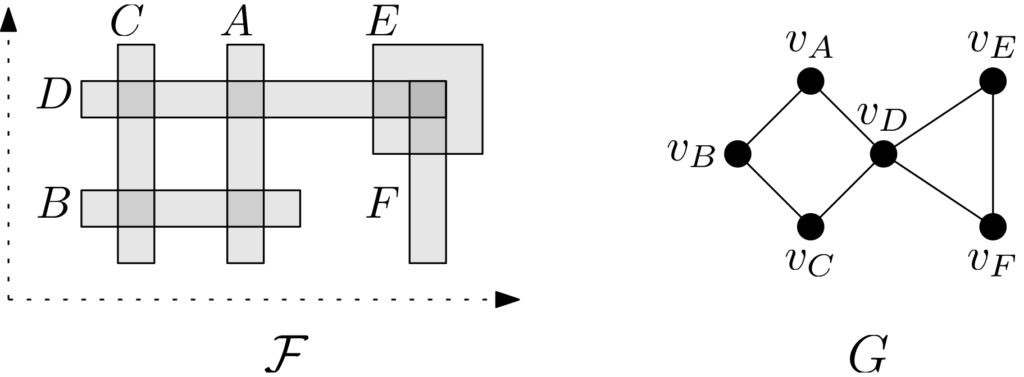
Few graphs classes with unbounded boxicity are known to have polynomial-time computable boxicity. The complements of block graphs have unbounded boxicity. In the work below, with Marco Caoduro and Will Evans, we design a polynomial-time algorithm to compute the boxicity of complements of block graphs. Our method also yields the analogous result for the threshold dimension (a similar parameter to boxicity involving threshold graphs). Our work suggests a general method that may yield efficient solutions to similar problems for other block-restricted classes.

(on arXiv Oct 2025): A polynomial algorithm to compute the boxicity and threshold dimension of complements of block graphs
(submitted to WALCOM 2026)

The underlying goal that interests me in the area of boxicity is to broaden the list of classes of graphs that permit polynomial-time boxicity computation. This can take the form of extending the approach from the above paper to other block-restricted classes, like cactus graphs.

Families of arithmetic progressions

An arithmetic progression of size k with common difference g has an interval of distance multiplicities, where gi occurs with multiplicity k-i. Reducing modulo n, a large subclass of modular arithmetic progressions satisfies the same distance multiplicity property (sometimes called “Erdős-deep” (ED)). For example: {0,3,6,9} modulo 13. These sets may be interpreted as musical rhythms with a timespan of n pulses and k onsets (note hits) and n-k rests. The distinct gaps between onsets each occur a distinct number of times, and so ED rhythms can be used to create compelling percussive structures with emergent patterns. Since music often involves overlapping rhythms, a natural goal is to construct and classify families of ED rhythms that preserve the same rich structure on the onset gaps collectively. That is, the union of internal distances of the constituent rhythms produces an interval of multiplicities.

Here is a musical demo that I wrote using ED rhythm families to organize the percussion parts:

In 1982, Paul Erdős posed the following planar geometry conjecture: for all k sufficiently large, there does not exist a configuration of k points in the plane such that the distances form an interval of multiplicities. There are known examples for k at most 8, but no proof is yet known. Below is an example configuration when k = 5.

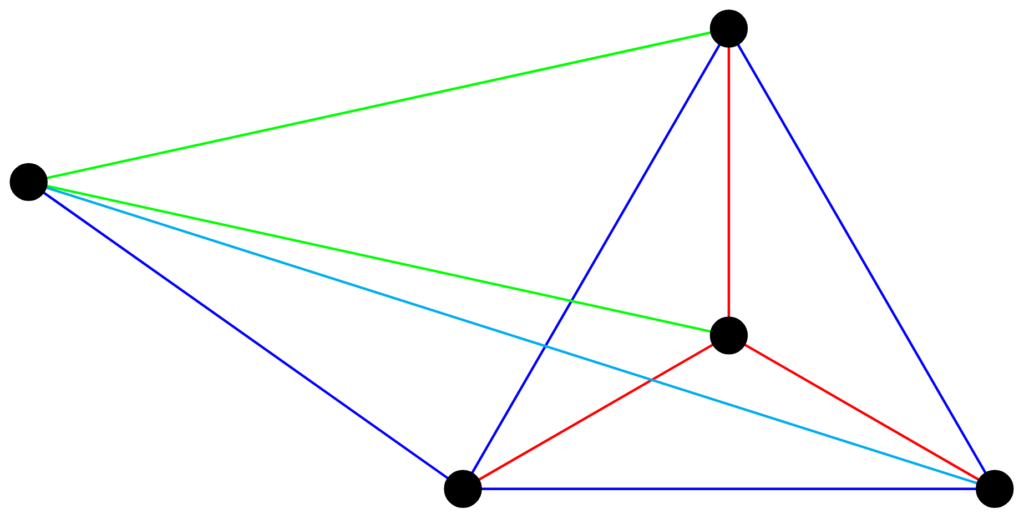
Similar questions can be asked in other finite metric spaces like in the set of integers modulo n with respect to the minimum difference metric. Inspired by this geometric problem and motivated by the application to musical rhythms, the following work, in collaboration with Peter Dukes, completely classifies the pairs of these modular arithmetic progressions, and also proves a general construction for larger families.

(on arXiv Aug 2022): Families of modular arithmetic progressions with an interval of distance multiplicities
(MR4573622; published in Integers Mar 2023)

I am broadly interested in similar AP family classification problems (and constructions), especially in the case where *both* the multiplicities and distances form an interval (this condition is sometimes referred to as “Winograd”).